CAUDALES MAXIMOS
La magnitud del caudal de diseño, es función directa del período de retorno que se le asigne, el que a su vez depende de la importancia y vida útil de la obra.
CAUDALES MAXIMOS – DISEÑO DE OBRAS
- Las dimensiones de un cauce
- Sistemas de drenaje
- Agrícola
- Aeropuerto
- Ciudad
- Carretera
- Muros de encauzamiento para proteger ciudades, plantaciones
- Alcantarillas
- Vertedores de demasías
- Luz en puentes
METODOLOGÍAS HIDROMETEOROLOGÍCAS DEL CÁLCULO DE CAUDALES MÁXIMOS
La hidro meteorología es el estudio de la meteorología aplicada a los parámetros hídricos. La teoría hidrometeorológica en general, comprende la observación, procesamiento y análisis del comportamiento de los elementos hídricos, fundamentalmente las descargas de los ríos y los volúmenes almacenados en reservorios y lagunas; y de los elementos meteorológicos, fundamentalmente la precipitación pluvial.En los modelos hidrometeorológicos se introducen los datos de entrada de cada cuenca, en particular los valores de precipitación, que posteriormente generarán información de caudal.
Se basan en considerar que el caudal máximo anual, es una variable aleatoria que tiene una cierta distribución.
Por ello los datos necesarios deben de ser los registros de caudales máximos anuales, ya que cuanto mayor sea el tamaño del registro, mayor será también la aproximación del cálculo del caudal de diseño el cual se calcula para un determinado período de retorno
Por lo general, en los proyectos donde se desea determinar el caudal de diseño, se cuenta con pocos años de registro, por lo que, la curva de distribución de probabilidades de los caudales máximos, se tiene que prolongar en su extremo, si se quiere inferir un caudal con un período de retorno mayor al tamaño del registro.
El problema se origina, en que existen muchos tipos de distribuciones que se apegan a los datos, y que sin embargo, difieren en los extremos. Esto ha dado lugar a diversos métodos estadísticos, dependiendo del tipo de distribución que se considere
MÉTODOS HIDROMETEOROLÓGICOS
Como definimos anteriormente los métodos meteorológicos se introducen los datos de entrada de cada cuenca, en este caso de la cuenca que se desea determinar el caudal de diseño para su posterior uso en una obra hidráulica. Existen varios métodos de este tipo como lo son:Sin embargo como sabemos, para la determinación del caudal de diseño se debe de conocer un cierto parámetro como lo es el “Periodo de retorno”.
PARÁMETROS PARA EL CÁLCULO DE CAUDAL MÁXIMO:
PERIODO DE RETORNO:
Para el caso de un caudal de diseño, el tiempo promedio en años, en que el valor del caudal pico de una creciente determinada es igualado o superado una vez cada “T” años, se le denomina período de retorno “T”.Según el Manual de hidrología, hidráulica y drenaje del Ministerio de Transportes y Comunicaciones:
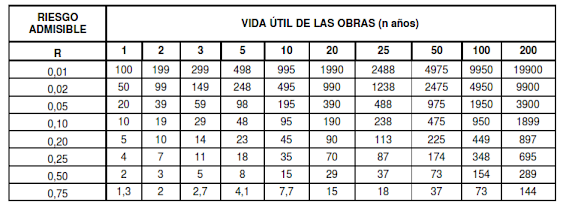
“Para adoptar el período de retorno a utilizar en el diseño de una obra, es necesario considerar la relación existente entre la probabilidad de excedencia de un evento, la vida útil de la estructura y el riesgo de falla admisible, dependiendo este último, de factores económicos, sociales, técnicos y otros”
La probabilidad de que un caudal máximo pase es:
P= Probabilidad de ocurrencia de un caudal Q
T= Periodo de retorno
El riesgo de falla admisible en función del período de retorno y vida útil de la obra está dado por:
n = número de años

Figura 1. Riesgo de por lo menos una
excedencia del evento de diseño durante la vida útil. (FUENTE: hidrología
aplicada (Ven te Chow)).
Considerando el Manual de Hidrológica, hidráulica y drenaje del Ministerio de Transportes y Comunicaciones, existe una Tabla N°2: Valores recomendados de riesgo admisible de obras de drenaje.
EJEMPLO:
TIEMPO DE CONCENTRACIÓN (TC):
Es el tiempo requerido por una gota para recorrer desde el punto hidráulicamente más lejano hasta la salida de la cuenca.Según el Manual de hidrología, hidráulica y drenaje del Ministerio de Transportes y Comunicaciones:
“Transcurrido el tiempo de concentración se considera que toda la cuenca contribuye a la salida. Como existe una relación inversa entre la duración de una tormenta y su intensidad (a mayor duración disminuye la intensidad), entonces se asume que la duración crítica es igual al tiempo de concentración”
Dado la siguiente definición del tiempo de concentración, el Ministerio de transportes y comunicaciones a establecido una tabla con las fórmulas usadas en el Perú, los cuales son, el método Kirpich, California Culverts Practice, Izzard, Federal Aviation Administration, Eciaciones de onda cinemática de Morgali y Linsley, Aron y Erborge,y Ecuación de retardo SCS.
 |
| TABLA No. 3 |
MÉTODOS USADOS PARA EL CÁLCULO DE CAUDALES MÁXIMOS:
1. MÉTODO DIRECTO
El caudal máximo se estima después del paso de una avenida, con base en datos específicos obtenidos en el campo. Los trabajos de campo incluyen:
1. Selección de un tramo del rio representativo, suficientemente profundo, que contenga al nivel de las aguas máximas.
2. Levantamiento de secciones transversales en cada extremo del tramo elegido y determinar:
A1, A2 = áreas hidráulicas
P1, P2 = perímetros mojados
R1, R2 = radios hidráulicos
3.- Determinar la pendiente S, de la superficie libre de agua con las huellas de la avenida máxima en el análisis.
4.- Elegir el coeficiente de rugosidad n de Manning de acuerdo a las condiciones físicas del cauce.
5.- Aplicar la fórmula de Manning:
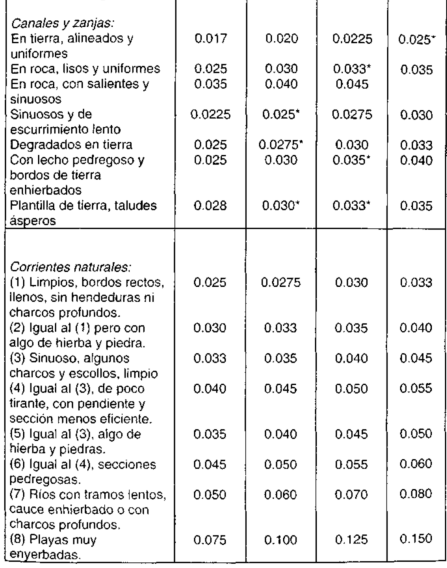
Para conocer los valores de “n” dados por Horton para ser usado en las formula de manning vaya a la Tabla N°4.
2. MÉTODO RACIONAL
El uso de este método, tiene una antigüedad de más de 100 años, se ha generalizado en todo el mundo, este método puede ser aplicado a pequeñas cuencas de drenaje agrícola, aproximadamente si no exceden a 13 km2.El caudal máximo se calcula por medio de la siguiente fórmula:
Q = caudal máximo, m/s
I= intensidad máxima de la lluvia, para una duración igual al tiempo de concentración, y para un periodo de retorno dado, en mm/h (Tabla N°6 y N°7)
C= coeficiente de escorrentía que depende de la cobertura vegetal, la pendiente y el tipo de suelo, adimensional.
A= área de la cuenca en hectáreas.
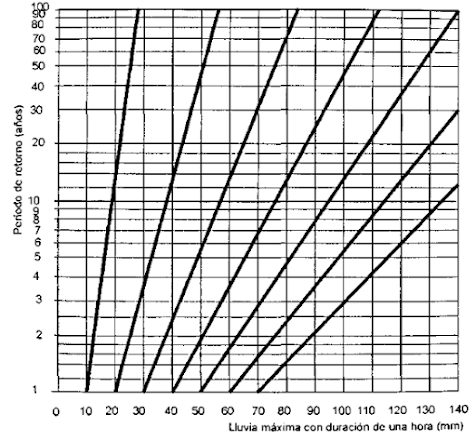 |
| TABLA No.6 |
 |
| TABLA No. 7 |
Coeficiente De Escorrentía: El coeficiente de escorrentía es la variable menos precisa del método racional, este representa una fracción de la precipitación total. Se debe escoger un coeficiente razonable para representar los efectos integrados de los factores que influyen en este.
Para los valores de coeficiente de escorrentía, se sabe que la cuenca se compone en diferentes superficies características, entonces el promedio de C se obtiene de una media ponderada, es decir:
 |
Figura
2. Pequeña tabla de coeficiente de escorrentía |
 |
| TABLA No. 5 |
EJEMPLO:
En una zona de limón se cuenta con 150 ha. En ella el 45% es bosque, con pendiente promedio del 8% y textura franco limosa, el resto del área es banano y pendiente de 4%. El 30% del área sembrada tiene una textura franco arenosa y el resto arcilloso. La distancia que existe desde el punto mas alejado del área, al punto donde se va evacuar el agua es de 1650 m. con desnivel de 12m.
Con los datos anteriores indicar cual será el caudal máximo utilizando el método racional para un periodo de retorno de 10 años con pendiente de 1%.
3. MÉTODO RACIONAL MODIFICADO:
Este método amplía el campo de aplicación del método racional, porque considera el efecto de la no uniformidad de las lluvias mediante un coeficiente de uniformidad, el caudal máximo de una avenida se obtiene mediante la expresión:Q=Caudal máximo, para un periodo determinado ( /s)
I=Intensidad máxima para un periodo determinado mm/s
A=Superficie de la cuenca
C=Coeficiente de escorrentía
CU=Coeficiente de uniformidad
- El coeficiente de uniformidad corrige el supuesto reparto uniforme de la escorrentía dentro del intervalo de cálculo de duración igual al tiempo de concentración en el método racional, este se puede determinar según la siguiente expresión:
4. MÉTODO DEL NÚMERO DE CURVA:
Este método fue desarrollado el SCS de EE.UU, se aplica a cuencas mediana como también a cuencas pequeñas.Este método es usado para estimar la escorrentía total a partir de datos de precipitación y otros parámetros de la cuenca de drenaje.
Un número de curva N=100, indica que toda la lluvia escurre, y un número N=1, indica que toda la lluvia se infiltra.
De la siguiente expresión:
F=infiltración real acumulada (L)
S=infiltración potencial máxima (L)
Q=escorrentía total acumulada (L)
Pe=escorrentía potencial o exceso de precipitación (L)
Se obtiene la siguiente fórmula:

Donde:
Q= escorrentía total acumulada, en cm
P= precipitación en cm
N= número de curva
En la ecuación se debe cumplir que N (P+5.08)-508>0, o P>508/N -5.08 Ver Tabla N°8 donde se muestra el gráfico de la ecuación.
 |
| TABLA No.8 |
CONDICION HIDROLOGICA:

GRUPO HIDROLOGICO DEL SUELO:
Grupo A, tiene bajo potencial de escorrentía
Grupo B, tiene un moderado bajo potencial de escorrentía
Grupo C, tiene un moderado alto potencial de escorrentía
Grupo D, tiene alto potencial de escorrentía
Para número de curva N, teniendo como dato el grupo hidrológico y la condición hidrológica se observa la Tabla N°8 ya antes visto para el número de Curva “N”.
CONDICIONES DE HUMEDAD ANTECEDENTE (CHA)
La condición o estado de humedad tiene en cuenta los antecedentes previos de la humedad de la cuenca, determinado por la lluvia total en el periodo de 5 días anterior a la tormenta.
El SCS usa 3 intervalos de CHA:
- CHA-I, Hay un mínimo potencial de escurrimiento
- CHA-ll, Es el promedio para el cual el SCS preparo la tabla N°8
- CHA-lll, hay máximo potencial de escurrimiento
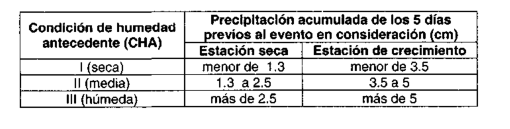 |
Figura 3. Condiciones de humedad
antecedente por la SCS. |

5. METODO DE CREAGER:
Este método, originalmente desarrollado por Creager, fue adaptado para el territorio peruano por Wolfang Trau y Raúl Gutiérrez Yrigoyen.La aplicación de este método permite la estimación de los caudales máximos diarios en cuencas sin información, para diferentes periodos de retorno, tomando el área de la cuenca como el parámetro de mayor incidencia en la ocurrencia de caudales máximos.
La fórmula empleada es la siguiente:

Donde:
• Qmax: caudal máximo para un periodo de retorno T seleccionado, en m3/s
• A: área de la cuenca aportante, en km2
• T: periodo de retorno, en años
• C1, C2: coeficientes adimensionales de escala, por regiones hidráulicas
• m, n: exponentes adimensionales, por regiones hidráulicas
6. METODOS EMPIRICOS
6.1. Método de Mac Math
Es uno de los tantos métodos utilizados para determinar el caudal máximo en cuencas.El caudal máximo se determina mediante la siguiente formula:
Q= caudal máximo con un periodo de retorno de T años, en m3/s.
C = factor de escorrentía de Mac Math, representa las características de la cuenca.
I = intensidad máxima de la lluvia, para una duración igual al tiempo de concentración tc y un periodo de retorno de T años, mm/hr.
A = área de la cuenca, en has.
S = pendiente promedio del cauce principal, en %.
De los parámetros que intervienen en esta fórmula, sobre el que se tiene que incidir, es sobre el factor C, el cual se compone de tres componentes, es decir:
C = C1 + C2 + C3
Donde:
C1 = está en función de la cobertura vegetal
C2 = está en función de la textura del suelo
C3 = está en función de la topografía del terreno
Para determinar estos valores nos basamos en la siguiente tabla:
MÉTODOS ESTADÍSTICOS PARA EL CÁLCULO DE CAUDALES

N= número de años de registro
Qi= Caudales máximos anuales registrados, m3/s
Qm= (∑_(i=1)^nQ_i )/N caudal promedio, m3/s
T= Periodo de retorno
σN,YN=constantes en función de N, ver Tabla N° 9 y 10
σQ= Desviación estándar de los caudales
Para el cálculo del intervalo de confianza (AQ) se hace lo siguiente:
Si: ∅=1-1/T varía entre 0.2 a 0.8, el intervalo de confianza se calcula con la fórmula:
Si: el intervalo se calcula como:
 |
| TABLA No. 9 |
 |
| TABLA No. 10 |
METODO DE GUMBEL EJEMPLO 9:
ΣQ2 = 40,595,065

Obtención de la ecuación del caudal máximo:



Cálculo del intervalo de confianza:

2 METODO DE NASH:
Nash considera que el valor del caudal para un determinado periodo de retorno se puede calcular con la ecuación:.
Donde:
a,b = constantes en función del registro de caudales máximos anuales.
Qmax = caudal máximo para un periodo de retorno determinado, en m3/s
T= periodo de retorno, años.
Los parámetros a y n se estiman utilizando el método de mínimos cuadrados, con la ecuación lineal: Q=a+bx, utilizando las siguientes ecuaciones:
- Se ordenan estos en forma decreciente, asignándole a cada uno un número de orden m.
- Al Qi máximo le corresponderá el valor 1, al inmediato siguiente 2, etc.
- Entonces el valor de del periodo de retorno para Qi se calculará utilizando la fórmula de Weibull con la ecuación:
Finalmente, el valor de cada se obtiene sustituyéndolo el valor de la ecuación (2) y (3)
- El intervalo dentro del cual puede variar el Qmax calculado por la ecuación (1), se obtiene como:
El caudal máximo de diseño correspondiente a un determinado periodo de retorno será al caudal máximo obtenido de la ecuación (1), mas el intervalo de confianza calculado según la ecuación (4).
Método de Nash Ejemplo 9
- Columna (1): número de orden
- Columna (2): caudales máximos ordenados en forma descendente
- Columna (3): período de retorno, obtenido con la formula de Weibull :
Columna (4): cociente



Cálculo del intervalo de confianza:Sustituyendo en la ecuación (6.37), se tiene:
3. MÉTODO LEBEDIEV:
• Este método está basado en suponer que los caudales máximos anuales son variables aleatorias Pearson tipo III.
• El caudal de diseño se obtiene a partir de la fórmula:
A=coeficiente que varía de 0.7 a 1.5, dependiendo del número de años del registro. Cuantos más años de registro haya, menor será el valor del coeficiente. Si N es mayor de 40 años, se toma el valor de 0.7
Cs=coeficiente de asimetría, se calcula como:
Cs= 3Cv para avenidas producidas por tormentas
Cs= 5Cv para avenidas producidas por tormentas en cuencas ciclónicas
- Entre estos valores, se escoge el mayor.
Cv= Coeficiente de variación, que se obtiene de la ecuación:

Er= coeficiente que depende de los valores de (ecuación 5) y de la probabilidad P=1/T, su valor se encuentra en la Tabla N°11.
K= coeficiente que depende de la probabilidad P=1/T, expresada en porcentaje de que se repita el caudal de diseño y del coeficiente de asimetría Cs.

Para obtener los valores de K, que es el coeficiente que depende de la probabilidad, en porcentaje, ver Tabla N°12
 |
| TABLA No. 11 |
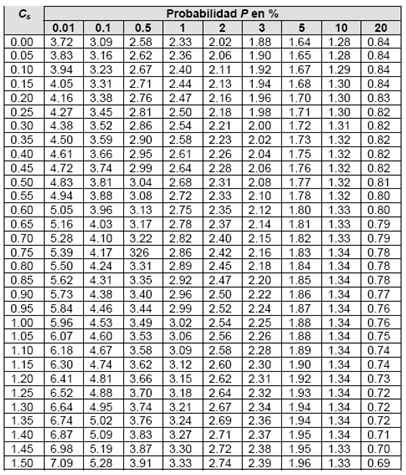 |
| TABLA No. 12 |
Método de Lebediev Ejemplo 9:
Para los mismos datos de la tabla 6.15, del ejemplo 6.7, calcular el caudal de diseño utilizando el método de Lebediev.
Obtención del caudal medio Qm
- Con P = 2 % y Cs = , de la tabla 6.17, se obtiene K = 3.12

- Para el período de retorno de 100 años, el valor de P es:














































No hay comentarios:
Publicar un comentario